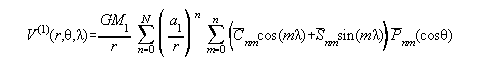
There is no such thing as "The" EGM96 geoid: Subtle points on the use of a global geopotential model

Dru A. Smith

National Oceanic and Atmospheric Administration/National Geodetic Survey,
1315 East-West Highway, Silver Spring Maryland, 20910
phone: 001- (301) 713-3202
fax: 001 - (301) 713-4172
email: dru@ngs.noaa.gov
Correspondence to: D. Smith

(This paper has been published in IGeS Bulletin No. 8, International Geoid Service, Milan, Italy, p. 17-28, 1998)

Abstract

The Earth's gravity potential field contains infinitely many level surfaces, each parallel to the others. The geoid is one such surface with a particular potential value, W₀. Spherical harmonic models of the Earth's external gravitational potential ("geopotential models") contain no explicit information about which level surface, out of the infinitely many that may be generated from the potential coefficients, is "the" geoid. Therefore, computing geoid undulations from a geopotential model requires additional information which should be carefully understood. Computer programs which compute gravimetric quantities from geopotential coefficients should contain prompts for this additional information. Submitted to the International Geoid Service (IGeS) is a FORTRAN program, geopot97 which accounts for all points in this paper except for the use of "correction coefficients" for topographic masses.

Introduction

At the recent joint meeting of the International Gravity Commission (IGC) and the International Geoid Commission (IGeC), numerous presenters did something which has occurred for years: they referred to such data sets as "The EGM96 geoid" and "The OSU91A geoid" (emphasis mine), among others, in a way that implied that "the geoid" is built into the spherical harmonic coefficients. The fact is, however, that no set of spherical harmonic coefficients of the Earth's external gravitational potential (which will be referred to as a "geopotential model") can be used by themselves to derive a model of geoid undulations. Four other pieces of information are required:

1. Choice of a normal gravitational potential field (encompassing the reference ellipsoid)
2. Choice of which level surface is "the" geoid
3. Knowledge of what permanent tide system the geopotential model refers
4. Knowledge of how the potential field acts inside topographic masses

Although well used for decades now, there still seems to be a general misunderstanding about how exactly geoid undulations are computed from a geopotential model. Very often, a program is run which is not fully documented and which is also missing one or more prompts for the information listed above. This paper hopes to briefly shed some light on what appears to be a frequently misunderstood issue. Finally, in an the spirit of "actions speak louder than words", a FORTRAN program, geopot97, has been submitted for testing to the International Geoid Service (IGeS) which can be used for rigorously computing gravimetric quantities using a geopotential model and the necessary additional information.

Anatomy of a geopotential model

Most modern geopotential models will be made available with four components:

1. The set of coefficients (usually called "C_nm" and "S_nm") from degree 2 to degree N
2. The adopted gravity-mass constant (GM₁) value used when creating the model
3. An equatorial scale factor, "a₁"
4. The permanent tide system of the model

These four pieces of information are enough to compute gravitational potential outside a sphere of radius r=a₁, using equation 1. In fact, the formula can be used accurately inside the sphere, as long as the evaluation point remains outside the topographic masses.

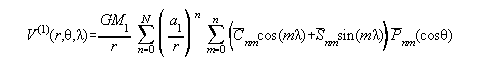
(1)

One should not put too much emphasis on "a₁" in equation 1. It is little more than a scale factor and does not represent the semi-major axis of any ellipsoid of interest to this problem.

Equation 1 yields gravitational potential, which is not, of course, the geoid undulation. To compute the geoid undulation requires the use of equation 1, and additional information, combined in the generalized Bruns equation.

The generalized Bruns equation

The generalized Bruns equation (to first order terms), which can be used to compute geoid undulations, is written as follows:

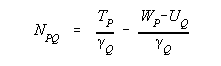
(2)

where (see also Figure 1):

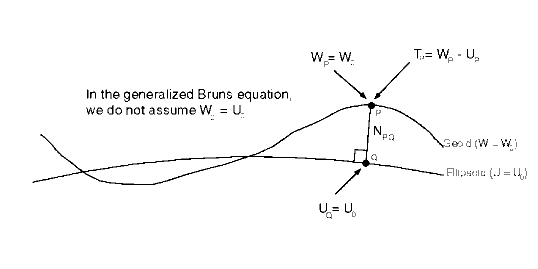
To see how a geopotential model is used in conjunction with the generalized Bruns equation and with additional information, we must expand equation 2, as shown below:

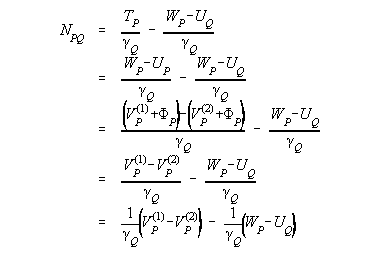
(3)

where F is the centrifugal potential (assumed identical for the true field and the normal field, thus the cancellation). V_P⁽²⁾ is the normal gravitational potential at P. Note that to use equation 3, there must be a-priori knowledge of the gravity potential on the geoid (W_P). In addition, the location of P itself must be known to evaluate V_P⁽¹⁾ and V_P⁽²⁾. That is, one must know the location of P, to use this formula to compute the location of P. As convoluted as that sounds, it is solved through a simple iterative computation in most programs which manipulate geopotential models (see Rapp, 1971).

It is seen in equation (3) that one must know the normal field (V_P⁽²⁾), as well as the level surface which will be called the geoid (W_P). In addition, the difference between V_P⁽¹⁾ and V_P⁽²⁾ contains the implicit assumption that both V_P⁽¹⁾ and V_P⁽²⁾ refer to the same tide system. If the tide systems are different from each other (or if either is different than the tide system in which you desire the output quantities computed), a correction should be applied to one or both of V_P⁽¹⁾ and V_P⁽²⁾. This is covered in a later section.

The Normal Potential Field

Equation 3 indicates a requirement for knowing the normal gravity potential, V⁽²⁾. Because a geopotential model is used to evaluate V⁽¹⁾, it will be useful to set up the normal potential field, V⁽²⁾, in a similar way, that is:

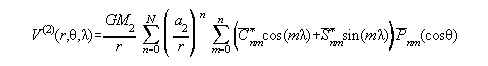
(4)

Note that a normal potential field consists purely of even zonal harmonics, so that most of the C^* and S^* terms (except C^*_n,0, where n is even) in equation 4 are zero.

Using the previous equations, we may write the disturbing potential at a point (T = V⁽¹⁾-V⁽²⁾) as:

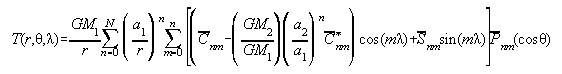
(5)

(Note here that we have made use of the fact that S^*=0 for all n and m). Often in practice, the ratios GM₂/GM₁ and (a₂/a₁)ⁿ are dropped except for the n=0 term. For terms where n>0, these ratios generally can affect the geoid computation by as much as 2 to 3 millimeters (effectively all in the n=2 term). Considering the miniscule computational burden of using the ratios, there is good reason for keeping the equation intact if one is interested in a truly "centimeter accuracy" geoid.

From the standpoint of geometry, the ellipsoid to which the geoid undulations will refer can be inferred from the normal potential field parameters. The semi-major axis of the reference ellipsoid is a₂. The flattening of the reference ellipsoid can be determined by the terms a₂, C^*_2,0, GM₂ and an adopted w (rotational velocity) through an iterative procedure to any needed accuracy (Rapp, 1971).

Choice of W₀

Equation 3 shows that a value of W_P (=W₀) needs to be known, or adopted, as the gravity potential on the level surface which is to be called "the" geoid. This seems to be one of the most confusing aspects of geoid computation, and, hopefully, will be clarified below.

One approach is to just pick a "reasonable" W₀ value. Recent estimates of W₀ have been published by the IAG Special Commission SC3 (IAG 1995). This method is the one chosen by the EGM96 team (Lemoine et al 1998, section 11.2), though they also point out the consistency between the adopted W₀ and a set of "a" and "f" values for an ellipsoid. This leads to the next method of W₀ determination, below.

Another, more round-about method is through the adoption of a so-called "best fitting ellipsoid", which is not far from the methods used by the IAG SC3 for computing their estimates of W₀. The logic for this method is as follows.

Assume that measurements of mean sea level (MSL) can be made through altimetry. Define "the geoid" (G) as the particular level surface which best fits (in the least squares sense, globally)to mean sea level. (A global fit is not truly possible, as altimetric measurements do not reach to the poles. For the purposes of this paper, "global" will be approximated by the range of the altimetry). By definition then, the mean dynamic topography (geoid/mean sea surface separation) should be zero, globally. Now define the "best fitting ellipsoid" (E_bf) as that ellipsoid which best fits to mean sea level (with semi major axis a_bf and flattening f_bf). By extension, therefore, the "best fitting ellipsoid" is also that ellipsoid which best fits to the geoid. As such, the "global" average separation between E_bf and G is zero. That is, if one were to average up, globally, the "geoid undulations, relative to the best fit ellipsoid" that average would be zero. For the global average geoid undulation to be zero, the following equations must be true (based on the generalized B runs equation):

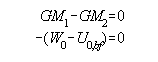
(6a) (6b)

Because this discussion has made no mention of either the true GM (GM₁) or the normal GM (GM₂), it may be adopted that the "best fitting ellipsoid" is part of a normal field where GM₂ = GM₁ (thus ensuring the validity of equation 6a). The real pay-off comes from equation 6b. Re-arranged, it reads:

(7)

Now, since the "best fitting ellipsoid" has been adopted, that means that the semi major axis, a_bf, and the flattening, f_bf, are known. If, as mentioned above, GM₂ is set equal to the best known GM₁ value, and a value of w is adopted, then U₀ may be computed by equation 8, and subsequently, from equation 7, W₀ is known! Equation 8 is a slightly re-arranged version of equation (2-61) in Heiskanen and Moritz (1967):

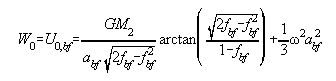
(8)

Both of the methods for choosing/calculating W₀ have the advantage that they are based on the most recent estimates about the size and shape of mean sea level and the geoid. There are other methods used, and these often have a critical mis-understanding of how to compute a geoid undulation.

Based on how rarely W₀ is explicitly stated in papers and presentations, there appears to be a lack of explicit knowledge about how to properly incorporate a choice of W₀, when using a geopotential model for computing geoid undulations. One misconception which occurs is that the GRS-80 ellipsoid is still a reasonable fit to the size and shape of the geoid. This is clearly not true, if centimeter accuracy is desirable. Recent estimates of the size of a best fitting ellipsoid differ in semi-major axis with GRS-80 by many decimeters (Rapp 1995, IAG 1995, Burša 1995). Additionally, recent estimates of the true GM for the Earth differ significantly from the GM of GRS-80 (McCarthy 1996, IAG 1995, Burša 1995). This does not make it impossible nor invalid to use GRS-80 as an ellipsoid to which geoid undulations refer -- it simply means that the degree zero terms arising from the differing GM values and the difference between U₀ and W₀ must be properly accounted for (errors of nearly a meter can occur through incorrect consideration of these terms -- see Smith and Small 1998). Other misconceptions are that the reference ellipsoid to which "the EGM96 geoid" can, or must, refer is somehow contained in the EGM96 information. For example, that the EGM96 "a₁" value is the semi-major axis of a reference ellipsoid, or that the flattening of the reference ellipsoid must be determined through the EGM96 C_2,0 term. These are both false. However, any software which does not explicitly prompt a user for information about which level surface is to be considered the geoid, must inherently be making some assumption about it. Most likely those assumptions will not match more recent estimates of the size and shape of the geoid.

Permanent Tide System

One subtle point, with a long history of study, but a short history implementation, is the permanent tide system. There are three systems in common use: Mean, Zero and Tide-free. In each system the contributions to the potential field, deformation of the crust, and best fitting ellipsoid to the geoid have their own definitions. And, while the shape of the geoid changes (from one tide system to another), the value of W₀ does not change from one system to another (IAG 1995). That is, the shape of the the level surface which best fits mean sea level in each of the three systems changes, but the potential of that level surface has an unchanged W₀ value.

Because both the potential field, and the normal potential field can be defined under three different permanent tide systems, it is mandatory that they refer to the same permanent tide system to in order to compute geoid undulations through the generalized Bruns equation. Thankfully this is fairly simple. The effect of changing a permanent tide system is seen only in the C_2,0 term. This goes for both the geopotential model (C_2,0) as well as the normal potential field (C^*_2,0). The change in the C_2,0 term is identical to the change in C^*_2,0, meaning that the change in shape of the geoid, between tide systems is identical to the change in shape of the ellipsoid. As such (and this is also seen through the Bruns equation) there is no difference between geoid undulations in any of the three permanent tide systems. This seems to be (but is not) in conflict with published formulas for transforming geoid undulations between tide systems (Lemoine, et al 1998, section 11.1; Rapp 1989). In those formulas, there is no change allowed to the reference ellipsoid. It is treated as a purely geometric quantity, unchanged by permanent tide systems, and only the geoid itself is allowed to change due to the permanent tide systems. Under these circumstances, the geoid undulation obviously changes from one tide system to another, but only represents the geometric change in the shape of the geoid (W=W₀) relative to an unchanging ellipsoid.

If the permanent tide system of V_p⁽¹⁾ differs from that of V_p⁽²⁾, then the two values should be brought into the same permanent tide system before proceeding with the generalized Bruns equation. This may be done by applying one, or both, of the following corrections to the C_2,0 term in the computation of V_p⁽¹⁾:

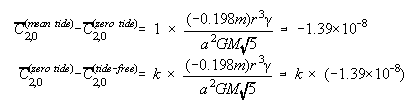
(9) (10)

where k is the (fundamentally unknowable) zero frequency Love number, which must be adopted. (For EGM96, k=0.3 was adopted). Although r and g have latitude dependence, this does not alter the effectively constant values computed in equations 9 and 10. These equations were derived from equations 1,3 and 4 combined with the following equations (for a change in geoid undulation relative to a fixed ellipsoid, Rapp, 1989):

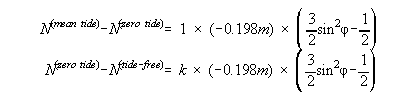
(11) (12)

Equations 9 and 10 also agree with the results found in (Melbourne et al, 1983).

Topographic Masses

It has been pointed out (Rapp 1997, Rapp 1992) that the potential computed from a geopotential model is inaccurate (over and above omission and commission errors) when the evaluation point lies inside the Earth's masses. These inaccuracies lead to incorrect geoid undulation computations which can be erroneous by up to 3 meters (Himalayas). Smith and Milbert (1999) show the error can exceed 1.5 meters in the Rocky Mountains. To compute more accurate geoid undulations, various methods have evolved, which all generally refer back to the same source -- Heiskanen and Moritz (1967, page 327, equation 8-102). The basic philosophy is that height anomalies (z) can be accurately computed at the surface of the Earth using the geopotential model, and then a correction (based on Bouguer anomalies, to first order) can be applied which yields the geoid undulation. When EGM96 was released, "correction coefficients" were also generated which would simulate this "Bouguer correction", for the express purpose of generating geoid undulations from the geopotential. Unfortunately there has been no published research on how to generate other gravimetric quantities (such as gravity anomalies) "in the masses" from geopotential models.

Although methods for applying the Bouguer correction are not encoded in program geopot97, there is one related "trick" which is coded in there, and that is for the fast evaluation of height anomalies at the surface of the Earth. As pointed out in Rapp (1997), if the radial distance (r) is unchanged then equation 5 (and any gravimetric quantities related to equation 5) may be quickly evaluated in latitude rows. This is an effect of using Clenshaw summation (Tscherning, Rapp and Goad 1983). When computing values at the geoid, the shallow gradients of the geoid allow a program to keep "r" constant for long stretches of latitude rows (while this is strictly untrue the evaluation point may be kept at a constant radius "r", which may deviate from the 'true' geoid position by as much as 10 meters without affecting the geoid or gravity anomaly computations in any significant way). The nature of quickly-changing topography, however, means that r must change quickly, and this significantly slows down the evaluation of equation 5. To get around this problem, one can evaluate disturbing potential (T), as well as the first and second upward derivatives of T, at the surface of the ellipsoid. Then, one can upward continue the disturbing potential to the surface of the Earth using the ellipsoid height, h. In computing the upward derivatives, the derivative with respect to h (not r) must be used to avoid centimeter level errors in the final height anomaly at the surface of the Earth. The derivatives of T with respect to r,q and l are simple to compute as part of the Clenshaw summation subroutine (ibid), and should be used to compute the derivative of T with respect to h through the following equation:

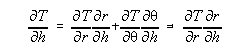
(13)

where:

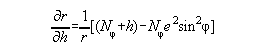
(14)

and N_f is the radius of curvature of the ellipsoid in the prime vertical, and e is the first eccentricity of the ellipsoid.

This method is detailed in Rapp (1997). Note that this method works, even though the values of T and its derivatives on the ellipsoid are "in the masses". This is due to the fact that equation 5 (and related equations for the derivatives) are continuous and smooth. Equation 5 may be evaluated anywhere (such as on the ellipsoid) without regard for whether it matches the "true" values. Because they are smooth and continuous, the use of T and its derivatives on the ellipsoid may be used in a Taylor expansion to reveal the value of T elsewhere (such as the surface of the Earth). As pointed out earlier, as long as the evaluation point is at or exterior to the Earth's surface, the potential computed from a geopotential model can be considered reliable. In effect, we use mathematics (without regard for the topographic mass issue) to implement:

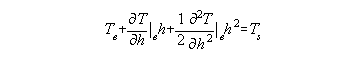
(15)

where the subscript "e" indicates the function evaluated at the ellipsoid, and "s" indicates the function at the surface of the Earth.

Running geopot97

A FORTRAN 77 program, geopot97, has been submitted to the IGeS for the computation of potential, and related quantities, from a geopotential model. Appropriate prompts for the normal field, the choice of W₀, and the permanent tide system are incorporated into that program. It is built around a Clenshaw summation routine (Tscherning, Rapp, Goad, 1983). Currently (version 0.4c) it will perform 11 different functions:

#1 - Given a spherical f/l and a value of gravity potential, find the radial distance to the surface of that potential

#2 - Given a geometric ellipsoid, an ellipsoidal f/l and a value of gravity potential, find the ellipsoidal height to the surface of that potential

#3 - Same as #1 but done on a grid of f/l values

#4 - Same as #2 but done on a grid of f/l values

#5 - Given a spherical f/l/r coordinate, compute gravity potential and gravitational potential at that point

#6 - Given an ellipsoidal f/l/h coordinate, compute gravity potential and gravitational potential at that point

#7 - Given a normal gravity field and an ellipsoidal f/l/h coordinate, compute gravity potential, gravitational potential, gravity, gravity anomaly, height anomaly, gravity disturbance, deflections of the vertical, and 3-D gradients of gravity at that coordinate

#8 - Given a normal gravity field and an ellipsoidal f/l coordinate and a defined W₀ value for the geoid, compute the geoid undulation and gravity anomaly for that location

#9 - Given a normal gravity field and a grid of ellipsoidal f/l coordinates and a defined W₀ value for the geoid, compute a grid of geoid undulations and/or gravity anomalies

#10 - Given a normal gravity field and a grid of ellipsoidal f/l coordinates, compute the height anomaly, and its first and second order upward derivatives, at the surface of the ellipsoid at the grid points

#11 - Given a gridded digital elevation model, compute a grid of gravity values at the surface of the Earth on that grid

Summary

Geopotential models have a long and important history in the geodetic community, specifically as a tool for computing geoid undulations. Often, the experience of using such models has been through provided programs -- sort of a "black box" approach (coefficients in, "geoid undulations" out). This approach is not generally valid due to the assumptions that such black box programs must make. This paper has argued that four important questions must be posed to properly compute geoid undulations, and fully document exactly what was computed. Those questions are:

1. What reference ellipsoid/normal potential field is used?
2. Which level surface, of the infinitely many, will be adopted as "the" geoid?
3. To what permanent tide system does the geopotential model refer?
4. How will I properly account for the topography?

In an attempt to answer the first three questions (which are inherently different than the fourth), a program geopot97 has been submitted to the IGeS for testing. It is hoped that future consistency in geoid computations may be achieved through this effort.

References

Burša, M, 1995: Primary and derived parameters of common relevance of astronomy, geodesy, and geodynamics. Earth, Moon and Planets, 69, pp. 51-63

Heiskanen, W.A. and H. Moritz, 1967: Physical Geodesy. W.H. Freeman, San Francisco, 364 pp

IAG, 1995: report of Special Commission SC3, Fundamental constants, International Association of Geodesy, Paris

Lemoine, F.G., et al, 1998: The Development of the Joint NASA GSFC and the National Imagery and Mapping Agency (NIMA) Geopotential Model EGM96, NASA Technical Report NASA/TP-1996\8-206861

McCarthy, D., 1996: IERS Technical Note 21, Observatoire de Paris

Melbourne, W, 1983: Project Merit Standards, U.S. Naval Observatory Circular. Report 167, Washington, D.C.

Rapp, R.H., 1971: Methods for the computation of geoid undulations from potential coefficients. Bulletin Géodésique, 101, p. 283-297

Rapp, R.H., 1989: The treatment of permanent tidal effects in the analysis of satellite altimeter data for sea surface topography. manuscripta geodaetica, 14(6), 368-372

Rapp, R.H., 1992: Global Geoid Solutions, in Geophysical interpretations of the geoid, ed. By Vaníek and Christou, CRC Press, Boca Raton, FL, pp. 57-76

Rapp, R.H., 1995: Equatorial radius estimates from TOPEX altimeter data, in Festschrift Erwin Groten, Institute of Geodesy and Navigation, Univ.

Rapp, R.H., 1997: Use of potential coefficient models for geoid undulation determinations using a spherical harmonic representation of the height anomaly/geoid undulation difference. Journal of Geodesy, 71(5), 282-289

Smith, D.A., and D.G. Milbert, 1999: The GEOID96 high resolution geoid height model for the United States, Journal of Geodesy, V. 73, No. 5, pp. 219-236
http://www.ngs.noaa.gov/PUBS_LIB/GEOID96_PAPER/geoid96_paper.html

Smith, D.A., and H.J. Small, 1999: The CARIB97 high resolution geoid height model for the Caribbean Sea, Journal of Geodesy, V. 73, No. 1, pp. 1-9
http://www.ngs.noaa.gov/PUBS_LIB/CARIB97_PAPER/carib97_paper.html

Tscherning, C.C., Rapp, R.H. and C. Goad, 1983: A comparison of methods for computing gravimetric quantities from high degree spherical harmonic expansions. Manuscripta geodaetica, 8, pp. 249-272