
Dru Smith
Updated: May 12, 1997
The Earth, like every other body of mass in the universe, generates gravitational potential in space (for any given location X,Y,Z, and time, t) [Equation 1]:

where (for later simplicity) x,y,z are a Cartesian co-ordinate system, centered at the center of masses of the Earth, with the z-axis aligned with a fixed direction in 3-dimensional space, and with a rotation matching that of the spinning Earth. We will use X,Y,Z to represent a specific location in our x,y,z frame. Gravitational potential also satisfies Poisson's equation at every point (X,Y,Z) in space, at any given time (t) [Equation 2]:
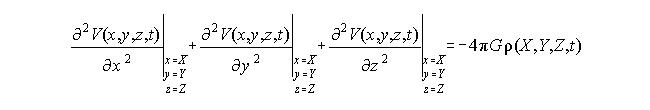
If we assume that outside of a certain closed surface, S, no masses exist (thus rho = 0), then we can say that outside of S the potential satisfies Laplace's equation [Equation 3]:

Laplace's equation is important to geodesists, because it must be valid everywhere outside of the geoid for Stokes' integral to hold. Stokes' integral is a fundamental geodetic formula used to compute geoid undulations from gravity anomalies [Equation 4]:
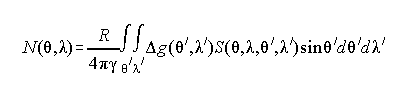
Where:
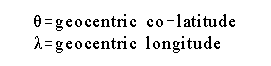
Note that Laplace's equation (3) is written with a time-dependence, but Stokes' integral (4) is not. For Stokes' equation to hold, we must somehow remove time-dependencies from Laplace's equation, as well as ensure that Laplace's equation holds everywhere outside of the geoid (which is a closed surface, "S").
In Laplace's equation, the time-dependence reminds us that the masses which generate potential are not constant in position over time. This fact is easily seen in equation (1), showing that for a fixed location in space (X,Y,Z), the density at that location has a time dependence. Specifically, the time variation of potential in space is dependent on two phenomena: The movement of distant masses (in the rotating x,y,z system), and the movement of local masses (in the rotating x,y,z system). A word of caution: These two phenomenon influence each other, and are therefore not entirely simple disjoint occurrences. An example of distant motion would be the orbits of the Sun and Moon, as well as their non-orbital apparent motion relative to a spinning Earth-centered x,y,z system. Two examples of local motion would be the rise and fall of the Earth's solid and fluid crust (due to the gravitational attraction of the Sun and Moon), and the local crustal motion not directly attributed to non-terrestrial gravitational influences (volcanism, weather, axis wobble).
Remember, we wish to modify Laplace's equation in two ways: 1) Remove time dependence and 2) make it valid everywhere outside of "S". Simple time averaging will generally solve the first problem. The second is a more subtle problem, because three portions of the time-averaged potential are non-zero. That is, they are "permanent". To understand this more fully, let us first define the various components of the potential [Equation 5]:
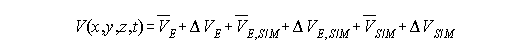
where:

The three time-constant values (with overbars) above are part of the "permanent" potential of the Earth. Both the "permanent" and "time dependent" potential can be grouped into three categories: non-tidal potential, direct tide potential, and indirect tide potential:

One may wonder whether the Earth, spinning alone in space would have time-varying motions of
its masses, relative to an Earth-centered rotating reference frame. However, geophysical,
glaciological, and tectonic issues aside, Woolard (1953) has shown that the spinning masses of a
rigid Earth, will move (wobble) relative to the axis of their rotation even with no other masses in
the Universe so long as the Earth's principle axes of inertia do not correspond to the axis of
rotation. (In addition, the axis of rotation, relative to 3-space also changes its orientation, so these
two combine to make masses move relative to our defined x,y,z system).
The direct and indirect time-dependent potentials are more clearly defined. The sun and moon
change their positions in time, relative to the Earth, inducing a direct tidal potential (the potential
of the Sun/Moon/etc. masses), and an indirect tidal potential (the potential of Earth masses,
where their motion is induced by the gravitational attraction of the moving Sun/Moon/etc.).
When computing geoid undulations using Stokes' integral (4), we assume a potential field with
no time variations. This implies that we have averaged in time or have modeled time-dependent
quantities that influence the potential field. However, as mentioned before, time-averaging does
not remove the "permanent" potential. This leads to three distinct types of "permanent tide
systems"; which describe how one deals with the three "permanent" potentials:
The mean tide system, where time-dependencies have been averaged, but no average ("permanent") tidal potentials have been removed [Equation 6]:
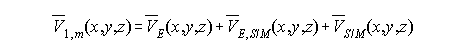
The zero tide system, where time-dependencies have been averaged, and the permanent direct tidal potential is removed [Equation 7]:
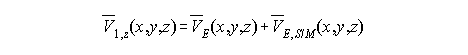
The non-tidal system, where time-dependencies have been averaged, and the permanent direct and indirect tidal potentials are removed [Equation 8]:
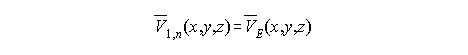
Now, back to Stokes' integral: if one assumes that the surface S is somewhere near the surface of the Earth (like the geoid), then masses external to S (the Moon, Sun, Planets, etc.) will invalidate Stokes' integral. As such, to satisfy Stokes' integral, we need to remove the existence, not the influence, of external masses. This statement means that the direct tidal potential of the Sun and Moon invalidate Stokes' integral, but the indirect potential (being the potential of Earth's masses) does not invalidate it. Or, more succinctly, the non-tidal and zero tide systems are valid for Stokes' integral. The mean tide system is not.
One final note: The existence of masses outside of the geoid, but on the Earth (the atmosphere, and the continental masses) also invalidate Stokes' integral. However, they are handled in a very different manner from the Sun/Earth/etc. masses, and are therefore not included here.
Got a question about this page?
Contact us in the USA at 301-713-3202 or at
dru@ngs.noaa.gov or
dennis@ngs.noaa.gov
.